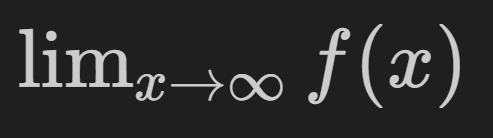Derivatives

Definition

The next step from limits of functions is derivatives. Here I’ll jump right into the formal definition:

Def. Let \(f: (a,b)\to \mathbb{R}\) be a function. We say \(f\) is differentiable at \(x_0\) if the following limit exists:

\[ f'(x_0) = \lim_{x\to x_0}\frac{f(x_0)- f(x)}{x_0 - x} \]

We call \(f'(x_0)\) the derivative of \(f\) at \(x_0\). If this limit exists for all \(x_0 \in (a,b)\), we say \(f\) is differentiable. In that case, the function \(f':(a,b) \to \mathbb{R}\) is called the derivative of \(f\) and is denoted: \(f' = \frac{d}{dx}(f) = \frac{df}{dx}\). We also call \(\frac{d}{dx}\) a differential operator.

Note that differentiablility is stronger than continuity. \(f\) is differentiable \(\implies\) \(f\) is continuous, but not the other way. \(f\) being continuous does not imply that \(f\) is differntiable.

As you know, the derivative of a function tells you the slope of the original function. This has an immense amount of uses, as you are no doubt already aware.

Calculating Derivatives

When actually calculating derivatives in practice, you memorize the derivatives of a few key functions (see function palooza) and the rules for calculating producrs and compositions of functions, which I’ll put below.

Linearity of the Derivative

Theorem. Let \(f,g : (a,b): \to \mathbb{R}\) be differentiable at \(x_0 \in (a,b)\) and let \(\alpha \in \mathbb{R}\).Then:

\[ \alpha(f + g)'(x_0) = \alpha f'(x_0) + \alpha g'(x_0) \]

Ignoring specification of \(x_0\) and using Leibinz notation, we can write this as:

\[ \alpha \frac{d}{dx}(f + g) = \alpha \frac{df}{dx} + \alpha\frac{dg}{dx} \]

Product Rule

Theorem. Let \(f,g : (a,b): \to \mathbb{R}\) be differentiable at \(x_0 \in (a,b)\). Then \(fg\) is differentiable at \(x_0\) with:

\[ (fg)'(x_0) = f'(x_0)g(x_0) + f(x_0)g'(x_0) \]

Ignoring specification of \(x_0\) and using Leibinz notation, we can write the product rule as:

\[ \frac{d}{dx}(fg) = \frac{df}{dx}g + f\frac{dg}{dx} \]

Chain Rule

Theorem. Let \(f:(a,b)\to (c,d)\) and \(g:(c,d)\to \mathbb{R}\) be functions. If \(f\) is differentiable at \(x_0\in(a,b)\) and \(g\) is differentiable at \(f(x_0)\), then \(g\circ f = g(f(x))\) is differentiable at \(x_0\) with:

\[ (g\circ f)'(x_0) = g'(f(x_0))f'(x_0) \]

Ignoring specification of \(x_0\) and using Leibinz notation we can write the chain rule as:

\[ \frac{d}{dx}g(f(x)) = \frac{dg}{df}\frac{df}{dx} \]

Power Rule

This one applies to only polynomials but is used so frequently I need to mention it.

Theorem. For \(a\in \mathbb{R} \setminus \{0\}\):

\[ \frac{d}{dx} x^a = ax^{a-1} \]