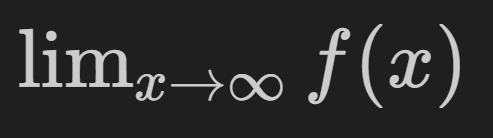Notation#
There are a few bits of notation that you need to know.
\(\in\) means “belongs to the set” or “is in.” \(a \in S\) means that \(a\) is in the set \(S\).
\(\forall\) means “for all” or “for every.” \(\forall x \in S\) means for all \(x\) in the set \(S\).
\(\exists\) means “there exists”
\(:=\) and \(\equiv\) and mean “is defined as” or “is denoted.” Ex. \(\vec{r}_{sep} \equiv \vec{r}_{obs} - \vec{r}_{source}\) means “The separation vector is defined as the observation position vector minus the source position vector.” (\(\dot{=}\) is also used for defining sometimes, I’m looking at you McIntyre)
Sets are usually defined within curly brackets \(\{ \} \). \(:\) or \(|\) within these brackets typically means “satisfying” or “such that,” (such that is sometimes abbreviated to s.t.)
\( E\subset S \) means \(E\) is a subset of \(S\), every element of \(E\) is also an element of \(S\)
\(f:A\to B\) denotes a function that maps from the set \(A\) to the set \(B\).
\(\setminus\) means “takeaway.” \(A\setminus \{x\}\) means \(A\) takeaway x, and is the set \(A\) with \(x\) removed.
\(\implies\) and \(\therefore\) mean “implies” and “therefore” respectively, and are often used interchangeably.
Examples#
The union of sets \(A\) and \(B\) is the set \(A\cup B := \{x:x\in A \text{ or } x \in B \} \)
The Intersection of sets \(A\) and \(B\) is the set \(A\cap B := \{x:x\in A \text{ and } x \in B \} \)
Some important sets:#
\(\mathbb{N}\) is the Natural Numbers. These are counting numbers \(1, 2, 3, ...\). Occassionaly these are defined as starting at \(0\) instead of \(1\), but starting at \(1\) is typical in the U.S.
\(\mathbb{Z}\) is the Integers. These are like the natural numbers, but they can also be negative: \(... -3,-2, -1, 0, 1, 2, 3...\)
\(\mathbb{Q}\) is the Rational Numbers. These are numbers that can be represented as a ratio of two integers: \(\mathbb{Q} := \{\frac{a}{b}: a,b \in \mathbb{Z} \text{ and } b \neq 0\}\)
\(\mathbb{R}\) is is the real numbers when you think of “numbers” these are probably what comes to mind. More on their definition is below.
\(\mathbb{C}\) is the complex numbers or imaginary numbers. These are the set \(\mathbb{C} := \{a + bi: a, b \in \mathbb{R} \}\), where \(i\) is the imaginary unit: \(i := \sqrt{-1}\)
\(\mathbb{R^n}\) is the set of n-tuples of real numbers: \(\mathbb{R}^n := \{(x_1, x_2, .... x_n): x_1, x_2 ... x_n \in \mathbb{R} \} \). \(\mathbb{R}^3\) for example is 3d space.