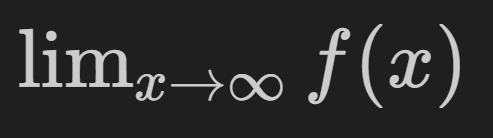Real Numbers

The real numbers are the set of all positive and negative numbers, as well as 0. We denote it as \(\mathbb{R}\). One can Construct the Reals, but its a bit technical and a physics major will (probably) never need to see that so I won’t go through that here.

Things you can do with real numbers: Add, Subtract, Multiply, Divide (except by 0), and compare (for 2 real numbers one must be greater than the other OR they are equal). All of the typical algebraic rules apply to real numbers.

Things you can’t do: Divide by 0, take square roots of negative numbers.

Another useful thing to note is that for two real numbers \(a\) and \(b\), if \(a\geq b\) and \(a \leq b\) then \(a=b\).

Bounds

For a subset \(\mathcal{Y}\subset \mathbb{R}\), an Upper-Bound of \(\mathcal{Y}\) is some \(b\in \mathbb{R}\) satisfying \(x\leq b\) for all \(x \in \mathcal{Y}\). If this \(b\) exists, we say \(\mathcal{Y}\) is bounded above.

For a subset \(\mathcal{Y}\subset \mathbb{R}\), a Lower-Bound of \(\mathcal{Y}\) is some \(b\in \mathbb{R}\) satisfying \(x\geq b\) for all \(x \in \mathcal{Y}\) If this \(b\) exists, we say \(\mathcal{Y}\) is bounded below.

The real numbers have the property that any subset \(\mathcal{Y}\subset \mathbb{R}\) that is bounded above has a least upper bound.

Intervals

For \(a,b\in\mathbb{R}\) satisfying \(a<b\), we call the following sets Intervals.

\[(a,b) := \{x\in\mathbb{R}: a<x<b \} \hspace{1cm} [a,b] := \{x\in\mathbb{R}: a\leq x \leq b \}\]

\[(a,b] := \{x\in\mathbb{R}: a<x\leq b \} \hspace{1cm} [a,b) := \{x\in\mathbb{R}: a\leq x < b \}\]

\[(a,\infty] := \{x\in\mathbb{R}: a<x \} \hspace{1cm} [a,\infty) := \{x\in\mathbb{R}: a\leq x \}\]

\[(-\infty,b] := \{x\in\mathbb{R}: x\leq b \} \hspace{1cm} (-\infty,b) := \{x\in\mathbb{R}: x < b \}\]

Triangle Inequality

This doesen’t come up in physics that often, but is still useful to know, The triangle inequality for real numbers states:

\[ \text{for a, b } \in \mathbb{R}, \space |a| + |b| \geq |a + b| \]