Function Palooza

In physics, there are a handful of functions that you should know by heart. I’ve outlined them (and their derivatives) here.

Constants and Polynomials

Function	Derivative
\(a\)	\(0\)
\(x^a\)	\(ax^{a-1}\)

Example

\[ \frac{d}{dx}(7x^4 + 3x^{5/2} + x + 4) = 7\frac{d}{dx}x^4 + 3\frac{d}{dx}x^{5/2} \frac{d}{dx} x + \frac{d}{dx} 4 = 28x^3 + \frac{15}{2}x^{3/2} + 1 \]

By linearity of the derivative and the power rule.

Real Valued Exponential

Function	Derivative
\(e^x\)	\(e^x\)

The exponential, denoted \(e^x\) or \(\exp{(x)}\) is probably the most important function in physics (I would argue in math in general as well). This is because it has the incredible property of being its own derivative.

Example

\[ \frac{d}{dx}e^{-2x} = -2e^{-2x} \]

By the chain rule. You should become very comfortable with this kind of derivative.

Complex Valued Exponential

Perhaps this isn’t the best time to introduce this, but its too important for me to leave out:

\[ e^{i\theta} = \cos(\theta) + i\sin(\theta) \]

This is called Euler’s Formula* .

More generally: $\( e^{x+iy} = e^x(\cos(y) + i\sin(y)) \)$

Natural Log

Function	Derivative
\(\ln{(x)}\)	\(\frac{1}{x}\)

The natural log is the inverse of the exponential, that is \(\ln{(e^x)} = x\) and \(e^{\ln{(x)}} = x\). \(\ln{(...)}\) is often denoted by just \(\log{(...)}\). Also, it is good to know that \(\ln{(1)} = 0\).

Properties (log rules)

Log properties
Powers	\(\ln{(x^a)} = a\ln{(x)}\)
Products	\(\ln{(xy)} = \ln{(x)} + \ln{(y)}\)
Division	\(\ln{\left(\frac{x}{y}\right)} = \ln{(x)} - \ln{(y)}\)

Exponentials of a different base

Now that we know \(e^x\) and \(\ln{(x)}\), we can define exponentials of any base:

\[ a^x = e^{x\ln{(a)}} \]

Trig Functions

Function	Derivative
\(\sin(x)\)	\(\cos(x)\)
\(\cos(x)\)	\(-\sin(x)\)
\(\tan(x)\)	\(\frac{1}{\cos^2(x)}\)

Recall that \(\tan(x) := \frac{\sin(x)}{\cos(x)}\).

The most important trig identity is: \(\sin^2 (x) + \cos^2(x) = 1\). I won’t write other ones down since they are easy to look up.

\(\sin(x)\) and \(\cos(x)\) are \(2\pi\) periodic, so they repeat every \(2\pi\). The function \(\sin(\omega x)\) then is \(\frac{2\pi}{\omega}\) periodic.

Exponential Form

Function	Exp. Form
\(\cos(\theta)\)	\(\frac{e^{i\theta} + e^{-i\theta}}{2}\)
\(\sin(\theta)\)	\(\frac{e^{i\theta} - e^{-i\theta}}{2i}\)

Inverse Trig functions

Here I favor the “arc” notation instead of \(^{-1}\) notation, since the latter can be confusing.

Function	Derivative
\(\arctan(x)\)	\(\frac{1}{1+x^2}\)
\(\arcsin(x)\)	\(\frac{1}{\sqrt{1-x^2}}\)
\(\arccos(x)\)	\(-\frac{1}{\sqrt{1-x^2}}\)

\(\arctan\) is probably the only one worth commiting to memory here. \(\arctan\) is technically a multi valued function, but almost always, you can assume that \(\arctan(x)\) will spit out a value in \((\pi/2,\pi/2)\).

Hyperbolic Trig Functions

These are less common, but still good to know as they do come up from time to time in physics.

Function	Derivative
\(\sinh(x)\)	\(\cosh(x)\)
\(\cosh(x)\)	\(\sinh(x)\)
\(\tanh(x)\)	\(\frac{1}{\cosh^2(x)}\)

Exponential Form

Function	Exp. Form
\(\cosh(x)\)	\(\frac{e^x + e^{-x}}{2}\)
\(\sinh(x)\)	\(\frac{e^x - e^{-x}}{2}\)
\(\tanh(x)\)	\(\frac{e^x - e^{-x}}{e^x + e^{-x}}\)

Even and odd functions

Many, but not all functions can be classified as even or odd. I’ll define these properties now:

Def.

\(f\) is even if \(f(-x) = f(x)\)

\(f\) is odd if \(f(-x) = -f(x)\)

Here is a classic example of even and odd functions:

import numpy as np
import matplotlib.pyplot as plt
x = np.arange(-3,3,0.05);plt.plot(x,5*x**2, label = 'even');plt.plot(x,x**3, label = 'odd')
plt.ylim(-10,10);plt.legend();plt.show()

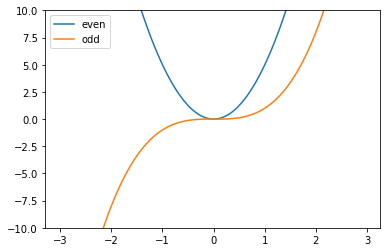
Even or odd?

Function	even or odd
\(\sin(x)\)	odd
\(\cos(x)\)	even
\(x^n, n\) even	even
\(x^n, n\) odd	odd
\(\cosh(x)\)	even
\(\sinh(x)\)	odd
\(\tanh(x)\)	odd
\(\arctan(x)\)	odd**

*Euler is pronounced oy·luh or oy·ler, you·ler is a common mispronunciation.

** again, \(\arctan(x)\) is multi valued, so one must be careful here.